Эволюция методов машинного обучения: от AlphaZero к AlphaProof и их применение в решении математических задач
Курновский Р.М.
📧 r.kurnovskii [at] gmail.com
Международный журнал прикладных и фундаментальных исследований, № 12, 2024
Аннотация
В данной статье подробно рассматриваются алгоритмы машинного обучения, заложенные в основу системы AlphaZero, а также их применение для решения сложных математических задач в системе AlphaProof. Целью работы являлось определение математических правил работы алгоритмов, благодаря которым они столь эффективны. В статье также рассматриваются перспективы и вызовы, связанные с применением нейронных сетей в научных исследованиях, особенно в области математических доказательств. Для этого был проведен всесторонний обзор научных источников и систематизация данных исследований. Было выявлено, что эффективность моделей была связана с оптимизациями алгоритмов поиска по дереву Монте-Карло и разработкой новых методов. AlphaProof использует методы обучения с подкреплением, разработанные на базе AlphaZero, которая изначально применялась для игр, таких как шахматы и го. Эти методы позволяют системе справляться с математическими задачами высокой сложности. Путем преобразования более миллиона задач из различных областей, включая алгебру, теорию чисел и геометрию, в формальные языки, такие как Lean, AlphaProof эффективно генерирует и проверяет решения, что делает ее мощным инструментом для математических исследований.
Ключевые слова: машинное обучение, нейронные сети, математические задачи, AlphaZero, AlphaProof
Abstract (EN)
This paper provides a detailed account of the machine learning algorithms that underpin the AlphaZero system, together with an analysis of their application to the resolution of complex mathematical problems in the AlphaProof system. The objective of this paper is to identify the mathematical principles underlying the algorithms that make them so effective. Furthermore, the paper investigates the potential and obstacles to utilizing neural networks in scientific enquiry, particularly within the domain of mathematical proofs. To this end, a comprehensive review of the scientific literature and systematic organization of the research data were carried out. It was determined that the efficacy of the models was contingent upon optimizations of Monte Carlo tree search algorithms and the development of novel methodologies. AlphaProof employs reinforcement learning techniques derived from AlphaZero, which was initially deployed in games such as chess and Go. These techniques enable the system to address mathematical problems of considerable complexity. By transforming over a million problems from diverse domains, including algebra, number theory, and geometry, into formal languages like Lean, AlphaProof can efficiently generate and verify solutions, making it a valuable tool for mathematical research.
Keywords: machine learning, neural networks, mathematical problems, AlphaZero, AlphaProof
Введение
25 июля 2024 г. команда Research компании Google DeepMind, занимающаяся разработкой и применением методов машинного обучения для решения математических задач, объявила о том, что их последние модели AlphaProof и AlphaGeometry 2 смогли решить задания сложнейшей международной математической олимпиады (65th International Mathematical Olympiad, IMO 2024) на уровне серебряного медалиста, отстав от порога для золотой медали на 1 балл [^1]. Стоит учесть, что, в отличие от реальных участников олимпиады, решающих задачи 4,5 часа, нейросети справились за 3 дня, но в скором времени ожидается многократное ускорение работы AlphaProof.
Бурный рост нейронных сетей в самых разных прикладных и фундаментальных областях за последние несколько лет привлекает внимание многих специалистов. Одним из важных вопросов является вопрос эволюции и развития методов обучения.
Цель работы заключается в определении ключевых технических и математических особенностей работы алгоритмов AlphaZero, AlphaProof и похожих моделей, благодаря которым они столь успешно решают математические задачи.
Материалы и методы исследования
Для проведения исследования была осуществлена систематическая оценка и анализ научных публикаций, посвященных эволюции методов машинного обучения с акцентом на разработку и применение моделей, таких как AlphaZero и AlphaProof, в решении математических задач.
Основным методом исследования стал литературный обзор, включающий поиск, отбор, классификацию и критический анализ научных статей, опубликованных в период с 2012 по 2024 г. Материалы для анализа были получены из международных научных журналов, включая Nature, IEEE, Science, а также публикаций Google DeepMind. Ключевыми словами поиска стали: AlphaZero, AlphaProof, «машинное обучение», «решение математических задач», «глубокое обучение».
Были рассмотрены статьи, охватывающие как технические аспекты алгоритмов, так и их применимость в математике и смежных областях. Критериями отбора статей служили актуальность исследований, детальное описание архитектур моделей AlphaZero и AlphaProof. Для структурирования данных применялась методология PRISMA, позволившая систематизировать процесс поиска, исключения дублирующихся данных и анализа релевантных источников.
Результаты исследования и их обсуждение
Используемые обозначения
| Обозначение | Значение |
|---|---|
| p | Вектор, каждая компонента pa которого – это вероятность принять данное положение при данном действии |
| v | Скаляр оценки результата |
| Θ | Гиперпараметры нейросети |
| fΘ | Функция нейросети при данных гиперпараметрах |
| s | Данное положение на доске (на примере игры в го) |
| a | Произведенный переход по дереву (действие) |
| Pr(a|s) | Вероятность занять данное положение на доске при данном действии |
| z | Скаляр, характеризующий результат игры |
| πa | Вектор вероятности произвести данный переход по дереву из данного начального положения |
| vt | Скаляр оценки результата игры на данном шаге |
| l | Функция потерь в методе градиентного спуска |
| T | Скаляр, характеризующий конечную позицию на дереве |
| c | Регулирующий параметр |
| cpuct | Скаляр, определяющий уровень исследованности данной ветви дерева |
| x | Параметр ошибки функции потерь, отличающий алгоритм PBT от алгоритма AlphaZero |
Все решения семейства Alpha компании DeepMind, включая AlphaFold 2, AlphaZero, AlphaGo, AlphaStar, AlphaTensor, AlphaCode и др., направлены на решение вычислительных прикладных и научных задач. Система AlphaProof представляет собой предварительно обученную на большой выборке математических задач и их решений модель с подкреплением AlphaZero.
Более миллиона математических рукописных задач из всех областей были переведены на формальный язык Lean с помощью Gemini [^1].
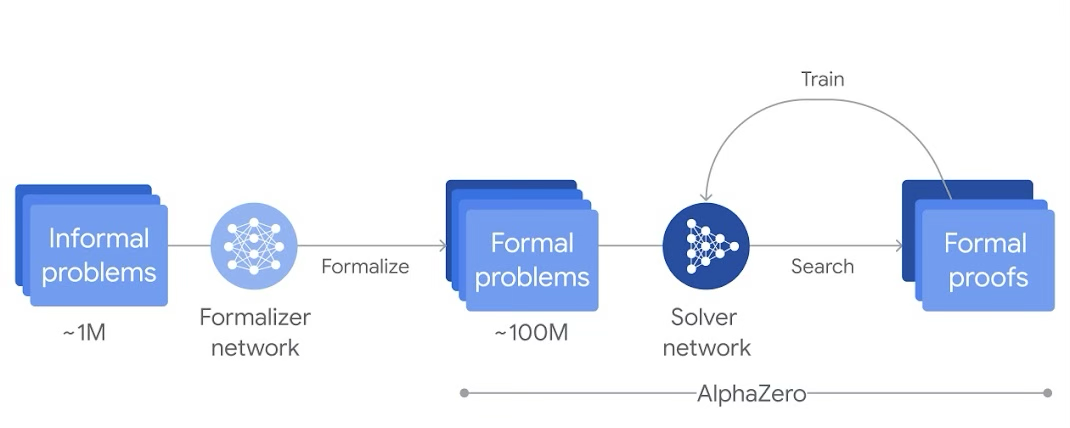
AlphaZero — это нейронная сеть, которая обучается за счет соревнования сама с собой в течение миллионов попыток с подкреплением. Процесс обучения сначала случаен, но быстро нейросеть корректирует параметры.
AlphaZero использует эвристический алгоритм поиска по дереву Монте-Карло (Monte Carlo Tree Search, MCTS) с нейросетевой оценкой.
Этот алгоритм отличается от классического MCTS тем, что применяет функции на основе deep learning: SL-policy, RL-policy, и оценку шансов на победу [^2].
Математические основы работы AlphaZero
AlphaZero использует нейросеть с архитектурой:
(p, v) = f_Θ(s)
Где:
p— вектор вероятностей действий:p_a = Pr(a|s)v— оценка результатаz:v ≈ E[z | s]
Параметры Θ подбираются обучением с подкреплением. В процессе симуляций:
- начальное состояние
s₀→ поиск по ветвям → возвращается векторπ_a = Pr(a | s₀)
Функция потерь:
l = (z - v)^2 - πᵀ log(p) + c ||Θ||²
Где:
T— конечная позиция на деревеc— параметр регуляризации
Байесовская оптимизация
Как и в AlphaGo Zero, используется байесовская оптимизация гиперпараметров, но они не меняются от игры к игре.
Каждое ребро дерева поиска (s, a) хранит:
(N(s, a), W(s, a), Q(s, a), P(s, a))
P(s, a)— априорная вероятностьN(s, a)— количество посещенийQ(s, a)— значение действияW(s, a)— суммарное значение
Выбор действия через доверительную границу
a_t = argmax_a [ Q(s_t, a) + U(s_t, a) ]
где:
U(s, a) = c_{puct} * P(s, a) * sqrt(∑_b N(s, b)) / (1 + N(s, a))
Обновление значений
При переходе по ребру (s, a):
Q(s, a) = ∑ V(s') / N(s, a), где s' — результат симуляции хода a из состояния s
Полная модель включает вероятностные поправки и тонкие настройки. После публикации AlphaZero велись активные исследования по оптимизации. Например, в [^6] (2020 г.) предложен популяционный метод (PBT).
Population Based Training (PBT)
- Используется несколько нейросетей с разными
Θ - Информация между ними передается и объединяется
- Слабые параметры заменяются лучшими
- Возможна ручная настройка параметров
Функция потерь в PBT:
l = (z - v)^2 + x - πᵀ log(p) + c ||Θ||²
Где x — параметр ошибки между z и v.
Применение AlphaProof
AlphaProof использует формализованные Lean-задачи (от Gemini). Это решает проблемы с:
- обработкой естественного языка,
- галлюцинациями нейросетей,
- логическими ошибками.
Для каждой задачи:
- Формализуется постановка.
- Генерируются сотни вариантов решений.
- Проверяются в Lean.
- Если решение неверно — перебирается следующее.
Lean использует:
- Calculus of Constructions (CoC),
- Calculus of Inductive Constructions (CiC).
Lean 4 поддерживает высокопроизводительное управление памятью, что ускоряет обучение AlphaProof.
Ограничения и перспективы
Пока нет:
- публикаций с тестами AlphaProof,
- данных о скорости, точности, областях математики.
Ожидаются уточнения с выходом второй версии. Тем не менее:
- AlphaProof может строго проверять сложные теоремы,
- особенно те, что используют абстрактные конструкции,
- перспективно и для генерации новых задач.
Теренс Тао на Oxford Mathematics Public Lectures отметил, что такие нейросети могут стать полноценными коллегами математика.
Заключение
AlphaZero и AlphaProof демонстрируют:
- значительный прогресс в методах ИИ,
- потенциал для решения фундаментальных задач.
AlphaProof — мощный инструмент в руках исследователя, а его развитие будет лишь ускоряться.
Для цитирования
@article{AlphaZero2AlphaProofEvolution,
author = {Курновский, Р.\,М.},
title = {Эволюция методов машинного обучения: от AlphaZero к AlphaProof и их применение в решении математических задач},
titleenglish = {Evolution of Machine Learning Methods: From AlphaZero to AlphaProof and Their Application in Solving Mathematical Problems},
journal = {Международный журнал прикладных и фундаментальных исследований},
journalenglish = {International Journal of Applied and Fundamental Research},
number = {12},
year = {2024},
pages = {41--45},
language = {russian},
annote = {В данной статье подробно рассматриваются алгоритмы машинного обучения, заложенные в основу системы AlphaZero, а также их применение для решения сложных математических задач в системе AlphaProof. Целью работы являлось определение математических правил работы алгоритмов, благодаря которым они столь эффективны. В статье также рассматриваются перспективы и вызовы, связанные с применением нейронных сетей в научных исследованиях, особенно в области математических доказательств. Для этого был проведен всесторонний обзор научных источников и систематизация данных исследований. Было выявлено, что эффективность моделей была связана с оптимизациями алгоритмов поиска по дереву Монте-Карло и разработкой новых методов. AlphaProof использует методы обучения с подкреплением, разработанные на базе AlphaZero, которая изначально применялась для игр, таких как шахматы и го. Эти методы позволяют системе справляться с математическими задачами высокой сложности. Путем преобразования более миллиона задач из различных областей, включая алгебру, теорию чисел и геометрию, в формальные языки, такие как Lean, AlphaProof эффективно генерирует и проверяет решения, что делает ее мощным инструментом для математических исследований.}
}